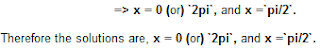Let us understand how sin2x works
The trigonometric identity is the identity of angles. The trigonometric identity is also called as circular identity. They are used for relating the angles of a triangle to the lengths of the sides of a triangle. The trigonometric identity is essential for the basic study of triangles and representation of periodic phenomena, surrounded by many other applications. One of the trigonometric identity is the sine identity. Question: Solve, sin2x × sin x = 0, to get the angle value of x from the double angle.
Question: Solve, sin2x × sin x = 0, to get the angle value of x from the double angle.
The trigonometric identity is the identity of angles. The trigonometric identity is also called as circular identity. They are used for relating the angles of a triangle to the lengths of the sides of a triangle. The trigonometric identity is essential for the basic study of triangles and representation of periodic phenomena, surrounded by many other applications. One of the trigonometric identity is the sine identity.
 Question: Solve, sin2x × sin x = 0, to get the angle value of x from the double angle.
Question: Solve, sin2x × sin x = 0, to get the angle value of x from the double angle.
Solution: Given that, sin2x × sin x = 0.
We know that, sin2θ = 2sinθ cosθ,
=> sin2θ = 2sinθ cosθ,
Now plug the value of sin2x in the equation sin2x + sin x = 0, we get,
=> (2sin x cos x) × sin x = 0,
=> 2sin x cos x × sin x = 0,
=> 2sin2x × cos x= 0,
Split the given expression into two terms, we get,
=> 2sin2x = 0, and sin x = 0,
=> sin2x = 0, and sin x = 0,
=> sin x = 0, and sin x = 0,
=> x = sin−1(0), and x = cos−1(0),
We know that, sin2θ = 2sinθ cosθ,
=> sin2θ = 2sinθ cosθ,
Now plug the value of sin2x in the equation sin2x + sin x = 0, we get,
=> (2sin x cos x) × sin x = 0,
=> 2sin x cos x × sin x = 0,
=> 2sin2x × cos x= 0,
Split the given expression into two terms, we get,
=> 2sin2x = 0, and sin x = 0,
=> sin2x = 0, and sin x = 0,
=> sin x = 0, and sin x = 0,
=> x = sin−1(0), and x = cos−1(0),
=> x = 0° (or) 360°, and x = 90°,