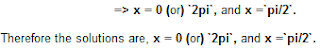Definition of Simultaneous Equations
A pair of "Simultaneous equations" is two equations which are both true at the same time. You have two equations which have two unknowns to be found.
Example
A man buys 3 fish and 2 chips for £2.80
A woman buys 1 fish and 4 chips for £2.60
How much are the fish and how much are the chips?
First we form the equations. Let fish be f and chips be c.
We know that:
3f + 2c = 280 (1)
f + 4c = 260 (2)
There are two methods of solving simultaneous equations. Use the method which you prefer:
Elimination
This involves changing the two equations so that one can be added/ subtracted from the other to leave us with an equation with only one unknown (which we can solve). We can 'change' the equations by multiplying them through by a constant- as long as we multiply both sides of the equation by the same number it will remain true.
In our above example:
Doubling (1) gives:
6f + 4c = 560 (3)
Since equation (2) has a 4c in it, we can subtract this from the new equation (3) and the c's will all have disappeared:
(3)-(2) gives 5f = 300 ∴ f = 60
Therefore the price of fish is 60p
So we can put f=60 in either of our original equations. Substitute this value into (1): 3(60) + 2c = 280 ∴ 2c = 100
c = 50
Therefore the price of chips is 50p
Substitution
The method of substitution involves transforming one equation into x = (something) or y = (something) and then substituting this something into the other equation.
So,Rearrange one of the original equations to isolate a variable.
Rearranging (2): f = 260 - 4c
Substitute this into the other equation:3(260 - 4c) + 2c = 280∴ 780 - 12c + 2c = 280 ∴ 10c = 500
∴ c = 50
Substitute this into one of the original equations to get f = 60 .
Harder simultaneous equations
To solve a pair of equations, one of which contains x2, y2 or xy, we need to use the method of substitution.
Example
2xy + y = 10 (1)
x + y = 4 (2)
Take the simpler equation and get y = .... or x = ....
from (2), y = 4 - x (3)
this can be substituted in the first equation. Since y = 4 - x, where there is a y in the first equation, it can be replaced by 4 - x .
sub (3) in (1), 2x(4 - x) + (4 - x) = 10
∴ 8x - 2x2 + 4 - x - 10 = 0
∴ 7x - 2x2 - 6 = 0
∴ 2x2 - 7x + 6 = 0 (taking everything to the other side of the equals sign)
∴ (2x - 3)(x - 2) = 0
∴ either 2x - 3 = 0 or x - 2 = 0
therefore x = 1.5 or 2 .
Substitute these x values into one of the original equations.
When x = 1.5, y = 2.5
when x = 2, y = 2
Using Graphs
You can solve simultaneous equations by drawing graphs of the two equations you wish to solve. The x and y values of where the graphs intersect are the solutions to the equations.
Example
Solve the simultaneous equations 3y = -2x + 6 and y = 2x -2 by graphical methods.
From the graph, y = 1 and x = 1.5 (approx.). These are the answers to the simultaneous equations.